圆周长公式,圆周长公式推导的几种方法?
圆周长公式,圆周长公式推导的几种方法?
圆周长公式推导的几种方法
没有什么推导过程,圆周率就是这么定义的。或者说,这是个大家都承认的事实(公理),你要是实在不相信,好像也没有什么方法证明这个事情。(如果你不相信1+1=2,也没法证明给你看1+1=2)
在古代,这个问题几乎是依赖于对实验的归纳。人们在经验中发现圆的周长与直径有着一个常数的比,并把这个常数叫做圆周率(西方记做π)。于是自然地,圆周长就是:C = π * d 或者C=2*π*r(其中d是圆的直径,r是圆的半径)。
割圆术的大致方法在中学的数学教材上就有。然而必须看到,它很大程度上只是计算圆周率的方法,而圆周长是C = π * d似乎已经是事实了,这一方法仅仅是定出π的值来。仔细想想就知道这样做有问题,因为他们并没有从逻辑上证明圆的周长确实正比于直径,更进一步说他们甚至对周长的概念也仅是直观上的、非理性的。
如果一定要你写推导过程
你可以用微积分相关的内容退出圆周长的公式,可是三角函数等等本来就建立在圆的周长、半径以及π的基础上,循环论证其实也站不住脚。
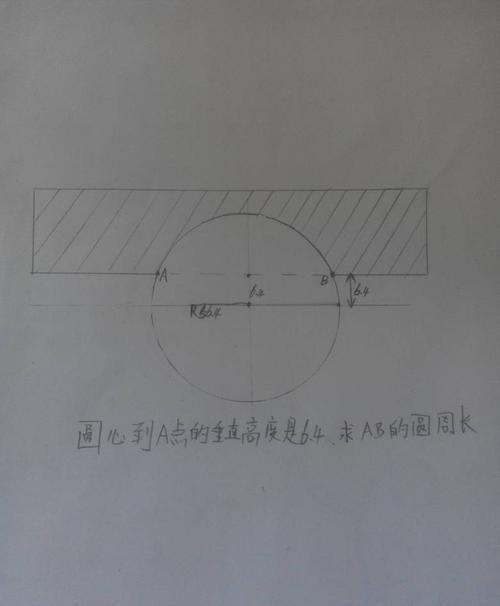
圆周长公式大全三年级
圆的周长公式:已知半径求周长,那么周长就等于圆周率乘以半径再乘以2已知直径求周长,那么周长就等于直径乘以圆周率。
科学家通过实验证明,圆的周长总是等于它的直径的3倍多一点,就把这三倍多一点儿叫做圆周率兀,派的取值是3.1415926……,兀值是个无理数所以圆的周长公式是:C=2兀r=兀d。
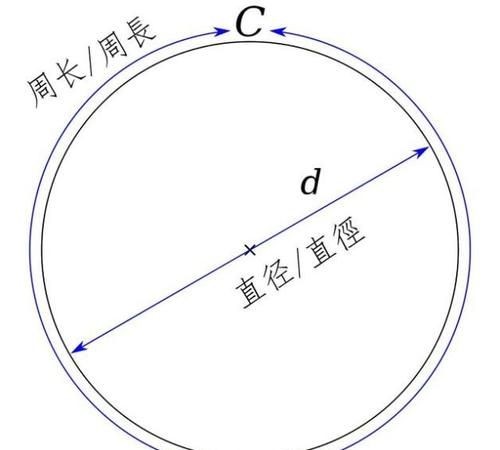
圆周长公式推导的几种方法
没有什么推导过程,圆周率就是这么定义的。或者说,这是个大家都承认的事实(公理),你要是实在不相信,好像也没有什么方法证明这个事情。(如果你不相信1+1=2,也没法证明给你看1+1=2)
在古代,这个问题几乎是依赖于对实验的归纳。人们在经验中发现圆的周长与直径有着一个常数的比,并把这个常数叫做圆周率(西方记做π)。于是自然地,圆周长就是:C = π * d 或者C=2*π*r(其中d是圆的直径,r是圆的半径)。
割圆术的大致方法在中学的数学教材上就有。然而必须看到,它很大程度上只是计算圆周率的方法,而圆周长是C = π * d似乎已经是事实了,这一方法仅仅是定出π的值来。仔细想想就知道这样做有问题,因为他们并没有从逻辑上证明圆的周长确实正比于直径,更进一步说他们甚至对周长的概念也仅是直观上的、非理性的。
如果一定要你写推导过程
你可以用微积分相关的内容退出圆周长的公式,可是三角函数等等本来就建立在圆的周长、半径以及π的基础上,循环论证其实也站不住脚。
圆周长公式大全三年级
圆的周长公式:已知半径求周长,那么周长就等于圆周率乘以半径再乘以2已知直径求周长,那么周长就等于直径乘以圆周率。
科学家通过实验证明,圆的周长总是等于它的直径的3倍多一点,就把这三倍多一点儿叫做圆周率兀,派的取值是3.1415926……,兀值是个无理数所以圆的周长公式是:C=2兀r=兀d。
圆周周长公式
公式2 C=2πr
公式1 C=πd
圆周长是指在圆中内接一个正n边形,边长设为an,正边形的周长为n×an,当n不断增大的时候,正边形的周长不断接近圆的周长C的数学现象,即:n趋近于无穷,C=n×an。
圆周长就是:或者(其中是圆的直径,是圆的半径)。
圆的周长公式和面积公式是啥汉字
圆的周长L=2πr(其中r为圆的半径,π为圆周率,通常情况下取3.14);圆面积公式是圆周率*半径的平方,用字母可以表示为:S=πr²或S=π*(d/2)²。(π表示圆周率,r表示半径,d表示直径)。
圆的面积和周长公式
相关计算
圆的半径:r
直径:d
圆周率:π(数值为3.1415926至3.1415927之间……无限不循环小数),通常采用3.14作为π的数值
圆面积:S=πr²;S=π(d/2)²
半圆的面积:S半圆=(πr²;)/2
圆环面积:S大圆-S小圆=π(R²-r²)(R为大圆半径,r为小圆半径)
圆的周长:C=2πr或c=πd
半圆的周长:d+(πd)/2或者d+πr